
During the last few years in Canada, concern has been growing over the rising provincial and federal deficits, which in no small part, can be linked to the escalating costs of education. However, this does not mean that Canadians as a group have become better educated and are topping the list in international comparison testing. Reports coming from the media have long suggested that as education costs have risen, levels of learning have fallen. As a result, public outcries have increased, demanding educational inquiries and reforms to prepare Canadian young people for the market demands of the 21st century, and to help them judge the opportunities and choices available to them. All provinces and territories are reviewing their programs and revising their school curricula. The quality and significance of education, along with how well people do in the lower grades, does affect the likelihood that they will go on to pursue a university education. Provincial and federal governments have commissioned studies to investigate how provinces compare with each other and to other countries. This study will investigate the level of university education for three Canadian provinces: Ontario, British Columbia, and Newfoundland, and attempt to find out if there are any inherent differences between them.
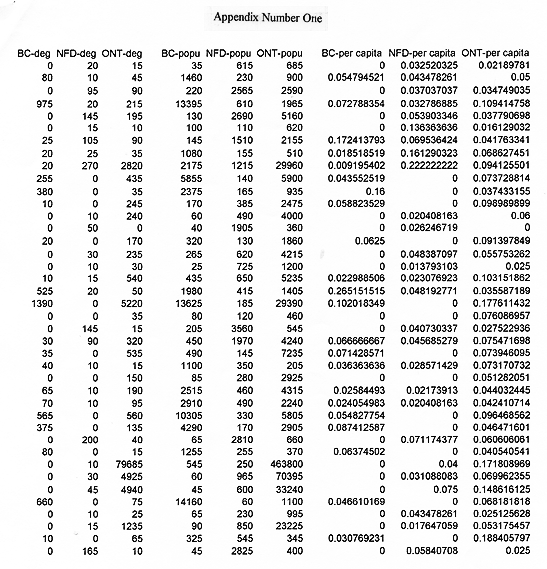
Three random samples of forty degree holders, one sample from each of the three provinces (British Columbia, Newfoundland, and Ontario) were collected using the geographic units of census subdivisions, including cities, towns, and municipalities. Sample data was provided from the 1991 Census and included two variables: first, that population numbers were limited to only those fifteen years of age and older; and secondly, that those studied, had at least one university degree. Testing will be done based on two separate criteria, namely, the unmodified degree numbers and the per capita figures, using an alpha level of .05. Two separate null hypotheses and two alternative hypotheses are needed since one F-test will compare the three provinces in the number of people with at least one university degree, and the other will compare the three provinces in degree holders per capita.
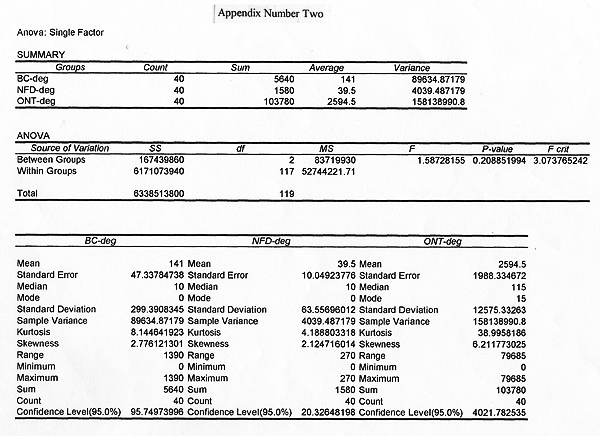
For the degrees, the null hypothesis is that there is no difference in the number of people having at least one university degree in the provinces of British Columbia, Ontario, and Newfoundland, while the alternative is that there is a significant difference in the numbers of people having at least one university degree in those three provinces. For the per capita figures, the null hypothesis is that in the three provinces, there is no difference in the number of people with at least one degree per capita. The alternative hypothesis states that there is a difference in the number of people with at least one degree per capita in those provinces, meaning that at least one province will have more or less degree holders per capita. Since looking at the sample means of each group will not necessarily give a realistic picture of significant difference, we must check the standard deviation to find the variance. When comparing more than two means simultaneously, analysis of variance (ANOVA) is used "to determine whether any differences among two or more means are greater than would be expected by chance" (Walsh 1990,124). The ANOVA test will provide data on the statistical significance of a relationship by examining the ratio of between-group variance/within-group variance, and give a F-score (O'Sullivan 1995,469).
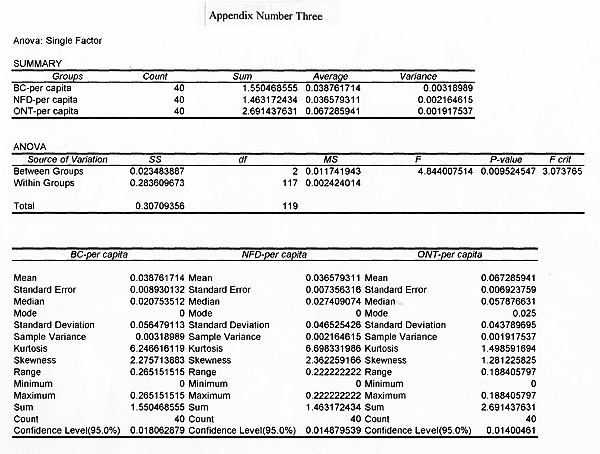
The first step is to compare the three provinces in the number of people with at least one university degree by using the analysis of variance (ANOVA). This results in a F-ratio of 1.587, which is clearly lower than the F-critical value of 3.074. Consequently, we will fail to reject the null hypothesis based on this test since the difference is not significant enough to say that it is based on anything but chance. Since there are no significant differences among the samples there is no point in examining the data any further. Simply counting the numbers of degrees that a province has is not enough to give a clear picture. The figures are inconclusive, but going further and testing for the F-score of per capita figures will provide a more realistic picture of the level of university education within these three test provinces. Using the per capita figures that were generated by the computer software (Appendix Number One), we can compare the three provinces in degree holders per capita.
This test results in an F value that clearly exceeds the F-critical value. We are forced to reject the null hypothesis and accept the alternative one, which states that there is a significant difference in the number of people with at least one degree per capita in British Columbia, Newfoundland, and Ontario. What it does not tell us is the pattern of difference. The HSD or Tukey Test must be used to establish where the difference is coming from in the per capita figures (see Appendix Number Four). The HSD value in this case is .0263.
The results of the HSD test are significant and suggest patterns of difference. First, the pairwise comparison of the absolute mean values of British Columbia and Newfoundland equal .0022, which is less than the HSD benchmark of .0263. This suggests that those two provinces are not significantly different from each other. Consequently, British Columbia and Newfoundland have similar numbers of people holding at least one degree per capita. The second phase of the pairwise comparisons shows a value of .0285 between British Columbia and Ontario, a number that is clearly greater than the HSD figure of .0263. This implies that there is a significant difference in the number of people with at least one degree per capita between British Columbia and Ontario, and in fact, is reinforced when one looks at the raw mean per capita figures for both provinces. Thirdly, the pairwise calculations between Newfoundland and Ontario produce the figure .0307, which is also greater than the HSD, demonstrating that a significant difference exists when comparing the number of degree holders per capita within those two provinces, with Ontario having more.
These findings are confirmed when they are compared with the confidence intervals of each province (see Appendix Number Four). Since the study is dealing "with sample data, one can state the probability that a parameter falls within a specified range called the confidence interval" (O'Sullivan 1995,352). We can be 95% certain that the number of people per capita in British Columbia with at least one degree will fall between .0207 and .0568, +/- 1.96 standard errors of the samples estimated. For Newfoundland, .0217 and .0568, and for Ontario they will fall between .0533 and .0813. As can be seen, there is great overlap between British Columbia's confidence intervals and Newfoundland's, which does confirm what the HSD found. In addition, there is little overlap when comparing the confidence levels of British Columbia and Ontario, and Newfoundland and Ontario. As A. Walsh has written in Statistics for the Social Sciences: With Computer Applications:
The objective of social science is to determine the source of this variability. We ask questions like "What is it that 'causes' or accounts for the observed differences between this group of people and that group of people, this individual or that individual" (Walsh 1990,125).
All that is left is to try to explain why these results have occurred. Is there a practical significance?
Why would British Columbia and Newfoundland have similar numbers of university degree holders per capita and fall far below the Ontario numbers? The major concern when using analysis of variance is that the samples are random. For instance, if the samples collected in British Columbia were not taken from all over the province, including the highly populated areas of Vancouver and Victoria, where one would expect to find many degree holders living, then the data may not truly reflect the population. In other words, the sample will not be free of bias. The results for British Columbia are particularly puzzling, (especially when looking at the standard deviation numbers for B.C. per capita) not because they show that the province has less degree holders per capita when compared with Ontario, but that the figures are so low and comparable to Newfoundland's. O'Sullivan and Rassel have pointed out that although random sampling is the goal, "this requirement is frequently violated . . . [and] the user should not infer a precise meaning from the statistic" (O'Sullivan 1995,369). Regardless, these statistics may provide some insight into the world of university education in Canada and bring about new avenues of research.
The first point to clarify is that education is a provincial responsibility under the Canadian Constitution. Educational systems and practices are directly affected by the policies, standards, and budgets that are set out by politicians and bureaucrats in the individual provinces. For many decades, Ontario was Canada's richest province, although the last few years have put Alberta in line for first place. Regardless, Ontario still spends more money per student on education than any other province per capita and has one of the lowest student/teacher ratios. Ontario is also known as the province that pays their teachers much more than all other provinces. Does this mean that the best Canadian teachers flock to Ontario for monetary reasons and provide the students there with a superior education? Further research is needed to answer this question, however, it can be said that lack of money does affect education programs and may deprive students of the diversity and depth of knowledge needed to spark an interest in a university education. Quality education in the lower grades seems to be a fundamental factor.
Newfoundland is considered a 'have not' province and has never had large sums of money for its education system. As a result, the quality of education in Newfoundland has never been as high as that of Ontario. The other factor is that for many years, teachers in the province were not required to have a university education at all. Some had a year of training. There are countless stories of the late Hon. Joseph R. Smallwood, one-time premier of Newfoundland and Father of Confederation, going to tiny outports to handpick future teachers and university professors when the university opened in the 1960s. He chose the brightest students in an area, but often they had not even finished high school themselves.
Other possibilities may shed some light on the provincial differences recorded in this study, including accessibility to a university. For instance, Ontario has more universities than any other province, while Newfoundland has only one and British Columbia few. If the majority of Newfoundlanders live in rural areas, far from the capital city and Memorial University, they will not think of leaving their hometowns to get a university education. Many cannot afford to move into the capital city. For some, getting a university education in Newfoundland is like moving to the mainland, something that many Newfoundlanders will not do. This has certainly affected the level of university education in the province. Incurring a student loan almost demands a move off the island for its repayment, since good paying jobs are very scarce in Newfoundland.
British Columbia has an extensive network of community colleges, but very few universities to serve its population. If a university education is preferred by a person living in northern British Columbia, it reduces the likelihood of that person attending a Vancouver or Victoria university because of the high rental costs in those areas. As well, British Columbia's economy has always been fairly stable, but the province has not had huge amounts of money to pour into their school system. Ontario's population does not have the same concerns, as the numbers and the quality of its provincial universities are great, significantly reducing the problems of access. These factors are particularly important as the trend of students living at home to keep post-secondary costs down continues.
Finally, there may be a higher probability that people living in British Columbia and Newfoundland will attend a technical school rather than a university. Looking at the numbers employed in natural resource-based industries in these two provinces seems to point in that direction. British Columbia has its farming, forestry, and fishing industries, plus a high concentration of jobs in the movie and music business. Also, construction jobs have been very plentiful in that province for the last decade due in no small part to the influx of Hong Kong immigrants. These kinds of jobs require technical training and not scholarly instruction. Likewise, Newfoundland is a province that has relied heavily on mining, forestry, fishing, and tourism-related industries for its economy, which requires technical training. Currently, the Hibernia oil field is one of the biggest employers, with workers getting their training at local technical colleges. In addition, dropout rates have always been high in the province, much of which is attributed to apprenticeships in the fishery at an early age. Also, both British Columbia and Newfoundland have very high illiteracy rates, with Newfoundland predictably having the highest illiteracy rate among provinces. William Thorsell, editor-in chief of the Globe and Mail has reported that 31 percent of British Columbia's population is illiterate (Thorsell 1996).
This differs greatly in Ontario, which historically has had an immigrant population coming from cultures that value education and the work ethic. They also have aspirations of succeeding and becoming financially successful in their new communities. To do that, university educations are more likely to be needed as professional and highly-skilled positions in corporations, law firms, and head offices of financial institutions warrant them. Lastly, it must be remembered that there are particular provinces that people leave in great numbers, and those that attract many new residents every year. Newfoundlanders have been migrating from the province in large numbers for many decades. They show up in the census figures of their new places of residence. For example, one of the largest populations of Newfoundlanders living outside the province live in the greater Toronto area. Some of them will have at least one degree or more.
It would appear as if the findings have a practical significance and that follow-up investigations may establish some important reforms. The world around us is changing very rapidly, especially when one considers computer technology and the Internet. Education must embrace new opportunities that have an impact on the job market and make the adjustments needed by providing better accessibility to university programs through new technologies. Education should be available for everyone, and governments need to work together to realize that vision. Would anyone say that a gifted student living in an outport in rural Newfoundland should not have the opportunity to access a good education? Education systems must work harder to include more of the population and focus on developing a life-long love for education and learning.




Related Papers
Correlation and Regression Bivariate Analysis