Librarians need to know how their facilities are meeting the needs of the community, and if existing levels of performance are appropriate for their users. They must also justify the money they receive from library boards and local government, including requests for bigger budgets. One way libraries evaluate their effectiveness is by doing surveys that ask library patrons a number of questions to test for a variety of variables the library is interested in focusing on. Overall, their goal is to increase library use by implementing services that are wanted and fulfilling their mission to provide their users with the resources they need. The St. Catharine's Public Library survey asked a series of approximately fifty questions, and the findings were analyzed for their significance.
One of the most popular ways to test for statistical significance in the social sciences is by using the chi square test of independence, which measures variables at the nominal and ordinal level, or categorical data (Walsh 1990,165). The chi square compares the frequency of expected values, "if chance alone were operating," against the observed (Rowntree 1991,187). It will not tell you how strong a relationship is or whether the relationship is positive or negative in value, but it does help researchers screen out those contingency tables that are significantly weak (O'Sullivan 1995,345). This report gives the findings of one small section of the survey results, which will be cross tabulated and tested for significance. The two variables are frequency of library visits and if patrons have a library card, with a null hypothesis stating that there is no significant relationship between the number of library visits a person makes and whether or not they have a library card. The alternative hypothesis is that there is a significant relationship between the number of library visits a person makes and whether or not they have a library card.
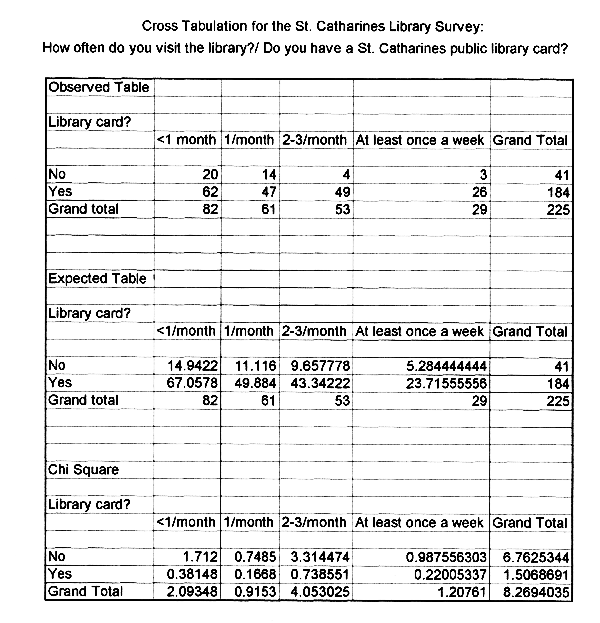
This study is testing if the observed frequencies of the crosstab table equal the frequencies we would expect under conditions of random chance, or if the same number of people having library cards use the library as often as those who do not. The first thing to do is organize the data, parse it, take out unwanted columns, and generate a crosstab or observed table. The columns represent one categorical variable; the rows the second variable. Contingency tables will show "the frequency or relative frequency of each value of the dependent variable for each value of the independent variable" (O'Sullivan 1995,378).
Step two is to remove the missing data, create a new table and an expected table, using the standard formula to calculate the expected values. The expected table represents what is expected if there were no relationship between the two variables; the frequencies expected if the null hypothesis was true. Since the use of chi square assumes that no expected cell frequency is less than five, this should be checked at this time. In this case, that is not a concern. Now everything is ready for the chi square test of independence, to see if these two variables have a statistically significant relationship, or if they are independent. The chi square score gives the proportional deviation between expected and observed frequencies.
By using the chi square formula (=(observed data expected data)^2/expected data) with the Excel software, the result is a value of 8.27. To find out if the computed chi square value of 8.27 is statistically significant, a chi square distribution table is used at an alpha level of .05 (with degrees of freedom of three), designating 7.815 the critical value, which is less than the calculated chi square value. This means that the value of 8.27 is significant at the 5% level, and should occur less than five in a hundred samples, if there is no relationship between the ownership of library cards and the frequency of library visits. Since the chi square is greater than or equal to the critical value, the null hypothesis is rejected, and the alternative hypothesis is accepted. Therefore, there is a significant relationship between the number of library visits a person makes and if they have a library card, and is representative of the population. What else can be said about the related variables?
Analyzation of the data uncovers some interesting points. First, if there were no association between library visits and library cards, then the same number of people, regardless of whether they have a library card or not, would visit the library as often. However, as the chi square test has shown, and by looking at the tables, this is obviously not true. The data shows that library visits increased if the user owned a library card. Inversely, there is evidence that those without a library card visited the St. Catharine's Public Library less often. In other words, 82% (184) of those reported have library cards and 18% do not.
Comparing cells in the expected table with those in the observed, expose some variations. For example, it was expected that of those reported who did not have a library card, 14.94 or 6.6% would visit the library less than once a month. However, the observed table shows that the number is actually twenty or 8.8% that visit the library less than once a month. Additionally, 30% of those with library cards were expected to visit less than once a month, but it was lower, at 27.5%. This frequency of less than once a month happens to be the mode of the table, or the value of the variable frequency of library visits that occurs most often. This was a surprise, since it was assumed that people with or without a library card would visit more than less than once a month.
It was expected that 5.28 or 2.3% of those without a card would visit the library at least once a week, but the observed shows that less than 1% visit at least once a week. Finally, it was expected that of those reported without a card, 4.3% (9.6578) would visit the library two or three times a month, when in fact, the observed was actually much lower at 1.7%. For the same frequency, the expected number was 19% or 43.34 with library cards, however, it was actually higher with 49 (22%) of those reported. These differences are too big to have arisen out of sampling error alone, meaning that there is a relationship in the population from which it was drawn. The smaller discrepancies noted between cells in the expected when compared to the observed could be the result of errors in the sampling process. As O'Sullivan and Rassel have said, "one cannot reasonably expect any one sample to be a completely accurate representation of the population" (O'Sullivan 1995,135). In addition, there seems to be a pattern occurring in the data. In the observed table, it is obvious that as the frequency of library visits increase, the numbers of people visiting drops off in both library card carriers and those without cards. For example, the numbers for those without library cards run from 8.8% to 6.2% to 1.7% to less than 1% as the frequency of library visits increase. For those with a library card, they run 27.5%, 21%, 22%, 11% as frequency increases. As one increases, the other decreases, which shows a definite relationship between the two variables - it means that they are related in the population.
Sample surveys do (or should) provide libraries with the data they need to evaluate their operations and plan for the future. Samples use a small number of people "to infer something about the larger population" (O'Sullivan 1995,107). Sample size is determined and the target audience is specified, which in this case is library users of the St. Catharine's Public Library. Question wording "determines the reliability and operational validity of measures" (O'Sullivan 1995,143). Both close-ended and opened-ended questions have their good and bad points. Close-ended questions are often chosen because they make data compilation easier, and people are more likely to answer them. Open-ended questions require writing out an answer and providing more details. Question wording can be problematic in both kinds of questions and should be carefully pretested. The number of questions asked is also a concern.
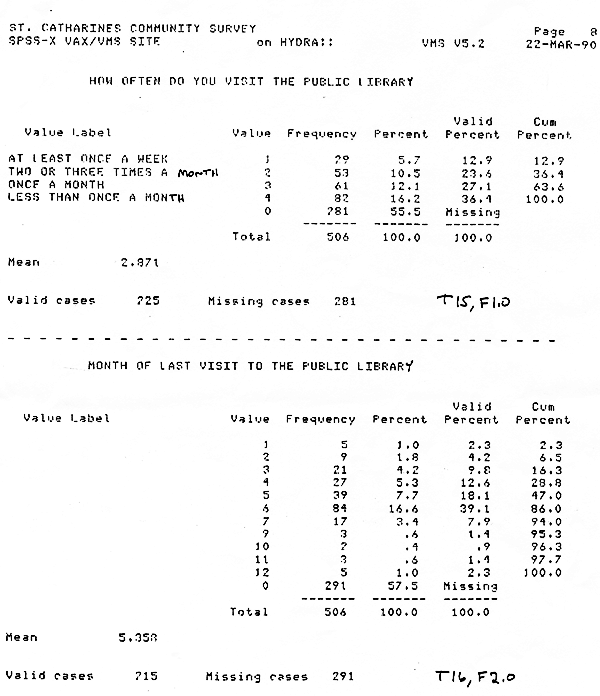
In this St. Catharine's survey, the participants were asked to answer close to fifty questions, which is quite a burden, especially nowadays when people are asked to do so many surveys on the telephone, through the mail, online, and in person. The number of questions should be kept to a minimum. If not, those answering may not concentrate on their responses, or they may skip some. Both of these scenarios can drastically effect the validity and reliability of a survey. For example, there were 281 missings from the question how often do you visit the public library, which could be symptomatic of question overload, since it is not a very difficult question to answer. Missings contribute to nonsampling errors and do have an impact on research findings. The larger the sample size, the greater the accuracy (O'Sullivan 1995,133). Chi square value, in particular, does not adjust for sample size, tending to become larger as sample size increases, therefore, the relationship could be even stronger than these figures show, since the pool was only 225.
The findings do not mean that having a library card causes people to go to the library more often, but there is certainly a relationship between the two variables. Since librarians are always interested in having their facilities used more often, it seems quite reasonable that having a get your library card campaign a couple of times a year is a smart, inexpensive, and easy way to increase the frequency of library visits. It is obvious that people go to the library for other things besides checking out materials, but it would be a good thing to increase library visits and circulation by offering library cards to patrons.



Related Papers
Correlation and Regression Bivariate Analysis